“A introdução de abstrações adequadas é a nossa única ajuda mental para reduzir o apelo à enumeração, para organizar e dominar a complexidade.” — Edsger Dijkstra”
Introdução
Este artigo tem como finalidade realizar uma discussão sucinta sobre algoritmos de busca e suas aplicações (contextos de uso), assim como apresentar e discutir a implementação de alguns algoritmos de busca cega, informada e complexa.
Discussão sobre algoritmos de busca em IA
Como visto no artigo Solução de Problemas em Inteligência Artificial, os algoritmos de busca desempenham um papel fundamental na área da inteligência artificial, pois são fundamentais para resolver problemas, tomar decisões e encontrar soluções. Segundo o professor Ricardo Araujo, doutor em Ciência da Computação pela Universidade Federal do Rio Grande do Sul, em sua publicação Algoritmos de Busca para Inteligência Artificial, pode-se dizer que, de maneira sucinta, um algoritmo de busca enumera possíveis soluções para um problema seguindo alguma sistemática que permita (e as vezes garanta) que uma solução desejada seja encontrada.
Outra informação extremamente relevante sobre este tema é o fenômeno conhecido como explosão do espaço de estados. Esse fenômeno refere-se a um desafio que surge em problemas de busca ou otimização, especialmente no contexto da AI. Sendo assim, tal evento ocorre quando o número de estados ou combinações possíveis em um espaço de busca cresce exponencialmente à medida que se avança na exploração desse espaço. Um bom exemplo desse fenômeno é quando analisa-se jogos como Sudoku, Xadrez e Go.
Diante do fenômeno acima, fica evidênte que para alguns problemas a busca cega é ineficiênte. É ai que entra a Busca Heurística (Busca Informada ou Busca Exaustiva com Informação), sendo uma heurística uma abordagem que fornece uma solução prática e aproximada quando a solução ideal é difícil ou impossível de se encontrar em tempo hábil. Segundo Ricardo, no contexto de buscas, uma heurística consiste em uma função que retorna, para um dado estado, o custo aproximado de chegar deste estado até uma solução.
Por outro lado, alguns problemas possuem complexidade tal que nem mesmo uma busca informada com heurísticas adequadas é capaz de resolver. É o caso de espaço de buscas complexos, como o problema do Caixeiro Viajante que envolve encontrar o caminho mais curto que visita todas as cidades exatamente uma vez e retorna à cidade de origem. Sendo assim, em um cenário do com um grande número de cidades, o espaço de busca cresce exponencialmente à medida que você adiciona mais cidades.
Outras aplicações de algoritmos de busca
O uso de algoritmos de buscas vai além da inteligência artificial. Tais algoritmos são bastante úteis, e as vezes fundamentais, em diversos outros contextos, tais como sistemas de navegação, logística, roteamento de redes, jogos, bioinformática, dentre diversos outros. Confira a seguir, alguns exemplos de sistemas os quais utilizam esse tipo de algoritmo.
- Google Maps, Moovit e Waze: utiliza algoritmos de busca para fornecer informações de navegação e encontrar rotas entre locais
- Projeto de um layout de circuito eletrônico em uma PCB: otimização do Layout, economia de recursos, adaptação a restrições, etc.
- Rede Nacional de Pesquisa (RNP): determinar as melhores rotas de rede, levando em consideração desempenho e segurança, para o tráfego de pesquisa e educação acadêmica no Brasíl.
Discussão sobre algoritmos genéticos
Segundo o primeiro artigo publicado no GMR Blog O que é uma AI?, a inteligência artificial é uma área interdisciplinar que envolve ciência da computação, biologia, psicologia, etc. Diante disso, com enfase às contribuições da biologia, o biomimetismo torna-se um forte aliado à produção de sistemas inteligêntes que imitam aspectos do comportamento humano, tais como aprendizado, percepção, raciocínio, evolução e adaptação. A Imagem 1 a seguir compara algumas tecnologias e suas respectivas inspirações na natureza.

Ref.: adaptado de ALGORITMOS GENÉTICOS: PRINCÍPIOS E APLICAÇÕES, página 1
Conforme evidenciado a cima, os Algoritmos Genéticos consistem em uma adaptação do princípio Darwiniano de seleção natural, onde o mais adaptado ao meio é capaz de sobreviver e deixar descendentes férteis. Contudo, para entender como tal princípio é aplicado à computação, é necessário fazer algumas analogias. A Imagem 2 a seguir apresenta uma comparação entre os elementos da natureza e suas respectivas representação no contexto dos Algoritmos Genéticos.
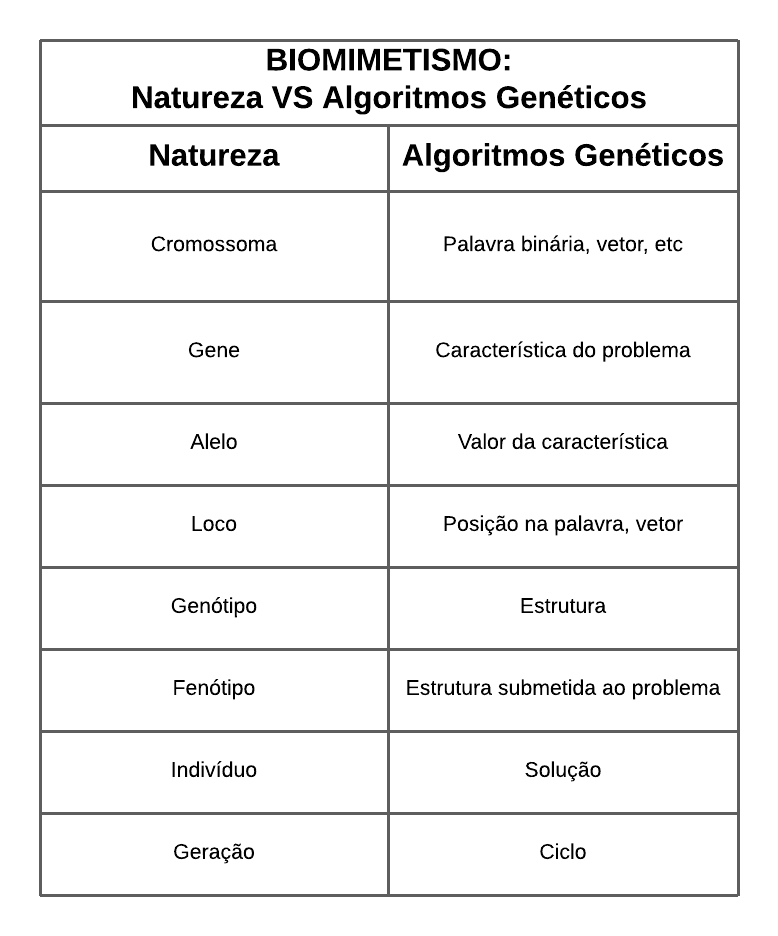
Ref.: adaptado de ALGORITMOS GENÉTICOS: PRINCÍPIOS E APLICAÇÕES, página 1
Algoritmos de Busca
A partir de agora, discutiremos alguns entre os principais algoritmos de proucura, considerando os diferentes tipos de busca abordados neste artigo: busca cega, informada e complexa. A Imagem 3 abaixo apresenta os algoritmos a serem apresentados.
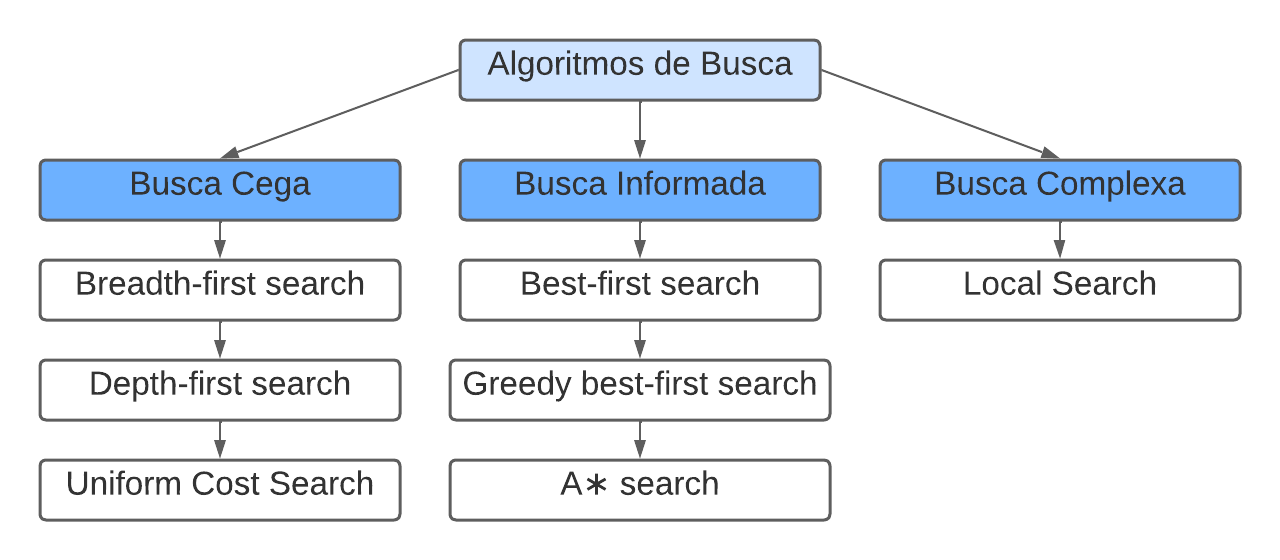
Ref.: autoria própria
Busca Cega
Como já sabemos, a busca cega consiste em uma abordagem na qual o agente explora um espaço de estados (ou espaço de soluções) sem ter informações detalhadas sobre a estrutura desse espaço ou a proximidade da solução desejada. Sendo assim, confira a seguir uma breve discussão e implementação sobre quatro diferentes algoritmos de busca não informada.
-
Breadth-first search (BFS): também conhecido como "Busca em Largura", esse algoritmo parte de um nó inicial e verifíca todos os elementos do próximo nível e, caso a resposta esteja no nível atual, o objetivo foi alcançado, caso contrário, procura-se no próximo nível e assim por diante. Se a resposta não estiver em nenhum dos níveis do grafo, é uma solução impossível. Essa estratégia utiliza uma queue (FIFO - Frist-in First-out) e um vetor de visitados como estrutura de dados auxiliares para se guiar entre os nós de um nível que ainda não foi visitado e, geralmente, é utilizada quando o problema em questão é muito pequeno e a complexidade do espaço não é considerada, além de ser bastante aplicado em buscas envolvendo árvores binárias.
Vantagens: retorna o caminho mais curto dentre as possibilidades de solução e nunca ficará preso em nós indesejados
Desvantagens: alto gasto de memória e tempo a medida em que o grafo aumenta de tamanho
EXEMPLO
Grafo:
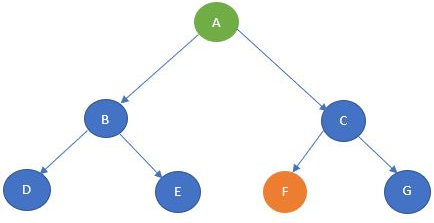
Ref.: Analytics Vidhya
Implementação da solução em python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
"""
# Ref.: https://www.analyticsvidhya.com/blog/2021/10/an-introduction-to-problem-solving-using-search-algorithms-for-beginners/
"""
graph = {
'A' : ['B','C'],
'B' : ['D', 'E'],
'C' : ['F', 'G'],
'D' : [],
'E' : [],
'F' : [],
'G' : []
}
visited = []
queue = []
goal = 'F'
def bfs(visited, graph, node):
visited.append(node)
queue.append(node)
while queue:
s = queue.pop(0)
print (s, end = "\n")
for neighbour in graph[s]:
if neighbour not in visited:
visited.append(neighbour)
queue.append(neighbour)
if goal in visited:
break
bfs(visited, graph, 'A')
-
Depth-first search (DFS): este algoritmo parte do estado inicial e explora cada caminho até sua maior profundidade antes de passar para o próximo caminho (por isso o nome "Busca em Profundidade"). Sendo assim, quando o algorimo encontra um vértice que não possui mais adjacência, ele retrocede para explorar outras opções, sendo este processo denominado backtracking.
Vantagens: demanda menos uso de memória e tempo em comparação a busca em largura.
Desvantagens: nem sempre garante uma solução e pode ficar preso em um loop infinito a medida em que se aprofunda em um grafo grande
EXEMPLO
Grafo:

Ref.: Analytics Vidhya
Implementação da solução em python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
"""
REF: https://www.analyticsvidhya.com/blog/2021/10/an-introduction-to-problem-solving-using-search-algorithms-for-beginners/
"""
graph = {
'A' : ['B','C'],
'B' : ['D', 'E'],
'C' : ['F', 'G'],
'D' : [],
'E' : [],
'F' : [],
'G' : []
}
goal = 'F'
visited = set()
def dfs(visited, graph, node):
if node not in visited:
print (node)
visited.add(node)
for neighbour in graph[node]:
if goal in visited:
break
else:
dfs(visited, graph, neighbour)
dfs(visited, graph, 'A')
- Uniform Cost Search (UCS): esse algoritmo pesquisa o gráfo dando prioridade máxima ao menor custo acomulado dentre os caminhos possíveis e, para isso, essa pesquisa uniforme de custos geralmente é implementada usando uma fila de prioridade. Sendo assilsm, é especialmente útil para encontrar o caminho mais curto em um grafo ponderado, isto é, os arcos (arestas) têm custos associados. Ele garante que a busca encontre o caminho de menor custo (quando possível), tornando-o ideal para problemas em que a otimização do custo é importante, como roteamento de mapas ou planejamento de caminhos em sistemas de navegação.
Vantagens: é considerada um entre os melhor algoritmo de busca para um grafo ponderado ou grafo com custos e, casa exista, encontra o menor caminho possível de um vértice à outro.
Desvantagens: não considera quantos passos são necessários para alcançar o caminho mais baixo. Isso também pode resultar em um loop infinito. </p>
EXEMPLO
Grafo:
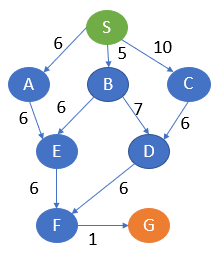
Ref.: Analytics Vidhya
Implementação da solução em python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
"""
REF: https://www.analyticsvidhya.com/blog/2021/10/an-introduction-to-problem-solving-using-search-algorithms-for-beginners/
"""
graph=[['S','A',6],
['S','B',5],
['S','C',10],
['A','E',6],
['B','E',6],
['B','D',7],
['C','D',6],
['E','F',6],
['D','F',6],
['F','G',1]]
temp = []
temp1 = []
for i in graph:
temp.append(i[0])
temp1.append(i[1])
nodes = set(temp).union(set(temp1))
def UCS(graph, costs, open, closed, cur_node):
if cur_node in open:
open.remove(cur_node)
closed.add(cur_node)
for i in graph:
if(i[0] == cur_node and costs[i[0]]+i[2] < costs[i[1]]):
open.add(i[1])
costs[i[1]] = costs[i[0]]+i[2]
path[i[1]] = path[i[0]] + ' -> ' + i[1]
costs[cur_node] = 999999
small = min(costs, key=costs.get)
if small not in closed:
UCS(graph, costs, open,closed, small)
costs = dict()
temp_cost = dict()
path = dict()
for i in nodes:
costs[i] = 999999
path[i] = ' '
open = set()
closed = set()
start_node = input("Enter the Start State: ")
open.add(start_node)
path[start_node] = start_node
costs[start_node] = 0
UCS(graph, costs, open, closed, start_node)
goal_node = input("Enter the Goal State: ")
print("Path with least cost is: ",path[goal_node])
Busca Informada
Outro tipo de algoritmo de busca abordado anteriormente é a busca informada. Como mencionado, essas técnicas de busca utiliza informações heurísticas para orientar a exploração em direção a soluções mais promissoras em problemas. Confira a seguir uma breve discussão e implementação sobre três exemplos de algoritmos de busca informada.
-
Best-First Search: este algoritimo utiliza função de avaliação (heurística) para optar pelo nó mais promissor entre os nós disponíveis antes de mudar para o próximo. Para isso, utiliza-se duas priority queue como estrutura de dado auxiliar, uma denominada ABERTA outra FECHADA. A primeira monitora os nós imediatos disponíveis para atravessar no momento, enquanto a segunda monitora os nós que já estão sendo transferidos, os quais formarão a resposta final. Sendo a sim, a cada iteração, verifica-se se o nó selecionado é o nó objetivo e, caso não seja, explora-se os nós adjacentes. Para isso, é necessário calcular suas estimativas heurísticas e ranquea-las na fila de prioridade, de forma que o nó mais promissor seja explorado em sequência, e assim por diante.
Vantagens: é ideal para os computadores avaliarem o caminho mais curto e apropriado através de um labirinto de possibilidades.
Desvantagens: demanda o cálculo de heurísticas, o que aumenta consideravelmente a compĺexidade computacional a medida em que o grafo aumenta.
EXEMPLO
Grafo:
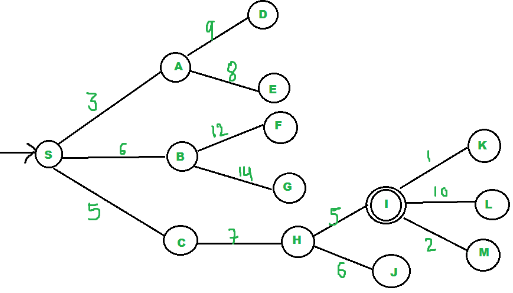
Ref.: GeeksforGeeks
Implementação da solução em python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
"""
# REF: https://www.geeksforgeeks.org/best-first-search-informed-search/
"""
from queue import PriorityQueue
v = 14
graph = [[] for i in range(v)]
# Function For Implementing Best First Search
# Gives output path having lowest cost
def best_first_search(actual_Src, target, n):
visited = [False] * n
pq = PriorityQueue()
pq.put((0, actual_Src))
visited[actual_Src] = True
while pq.empty() == False:
u = pq.get()[1]
# Displaying the path having lowest cost
print(u, end=" ")
if u == target:
break
for v, c in graph[u]:
if visited[v] == False:
visited[v] = True
pq.put((c, v))
print()
# Function for adding edges to graph
def addedge(x, y, cost):
graph[x].append((y, cost))
graph[y].append((x, cost))
# The nodes shown in above example(by alphabets) are
# implemented using integers addedge(x,y,cost);
addedge(0, 1, 3)
addedge(0, 2, 6)
addedge(0, 3, 5)
addedge(1, 4, 9)
addedge(1, 5, 8)
addedge(2, 6, 12)
addedge(2, 7, 14)
addedge(3, 8, 7)
addedge(8, 9, 5)
addedge(8, 10, 6)
addedge(9, 11, 1)
addedge(9, 12, 10)
addedge(9, 13, 2)
source = 0
target = 9
best_first_search(source, target, v)
# This code is contributed by Jyotheeswar Ganne
-
(GBeFS): este algoritmo concentra-se em explorar nós que estão mais próximos do objetivo, com base em uma heurística que fornece uma estimativa do custo para atingir o objetivo. Contudo, ele não considera o custo total até o momento, apenas a proximidade ao objetivo. Logo, o Greedy Best-First Search escolhe o nó que parece ser o "melhor" com base na heurística, sem considerar o passado. Isso pode levar a soluções rápidas em alguns casos, mas não garante a solução ótima.
Vantagens: sua implementação é relativamente simples, além de ser rápido, eficiênte e requisitar pouca memória.
Desvantagens: não garante uma solução ótima, pois pode negligenciar áreas do espaço de busca que podem conter soluções melhores
EXEMPLO
Grafo:
Ref.: AlgorithmExamples
Implementação da solução em python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
"""
REF: https://python.algorithmexamples.com/web/graphs/greedy_best_first.html
https://en.wikipedia.org/wiki/Best-first_search#Greedy_BFS
Gráfico modelado em matriz de adjacência
"""
from typing import List, Tuple
grid = [
[0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0], # 0 are free path whereas 1's are obstacles
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0],
[1, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0],
]
delta = ([-1, 0], [0, -1], [1, 0], [0, 1]) # up, left, down, right
class Node:
"""
>>> k = Node(0, 0, 4, 5, 0, None)
>>> k.calculate_heuristic()
9
>>> n = Node(1, 4, 3, 4, 2, None)
>>> n.calculate_heuristic()
2
>>> l = [k, n]
>>> n == l[0]
False
>>> l.sort()
>>> n == l[0]
True
"""
def __init__(self, pos_x, pos_y, goal_x, goal_y, g_cost, parent):
self.pos_x = pos_x
self.pos_y = pos_y
self.pos = (pos_y, pos_x)
self.goal_x = goal_x
self.goal_y = goal_y
self.g_cost = g_cost
self.parent = parent
self.f_cost = self.calculate_heuristic()
def calculate_heuristic(self) -> float:
"""
The heuristic here is the Manhattan Distance
Could elaborate to offer more than one choice
"""
dy = abs(self.pos_x - self.goal_x)
dx = abs(self.pos_y - self.goal_y)
return dx + dy
def __lt__(self, other) -> bool:
return self.f_cost < other.f_cost
class GreedyBestFirst:
"""
>>> gbf = GreedyBestFirst((0, 0), (len(grid) - 1, len(grid[0]) - 1))
>>> [x.pos for x in gbf.get_successors(gbf.start)]
[(1, 0), (0, 1)]
>>> (gbf.start.pos_y + delta[3][0], gbf.start.pos_x + delta[3][1])
(0, 1)
>>> (gbf.start.pos_y + delta[2][0], gbf.start.pos_x + delta[2][1])
(1, 0)
>>> gbf.retrace_path(gbf.start)
[(0, 0)]
>>> gbf.search() # doctest: +NORMALIZE_WHITESPACE
[(0, 0), (1, 0), (2, 0), (3, 0), (3, 1), (4, 1), (5, 1), (6, 1),
(6, 2), (6, 3), (5, 3), (5, 4), (5, 5), (6, 5), (6, 6)]
"""
def __init__(self, start, goal):
self.start = Node(start[1], start[0], goal[1], goal[0], 0, None)
self.target = Node(goal[1], goal[0], goal[1], goal[0], 99999, None)
self.open_nodes = [self.start]
self.closed_nodes = []
self.reached = False
def search(self) -> List[Tuple[int]]:
"""
Search for the path,
if a path is not found, only the starting position is returned
"""
while self.open_nodes:
# Open Nodes are sorted using __lt__
self.open_nodes.sort()
current_node = self.open_nodes.pop(0)
if current_node.pos == self.target.pos:
self.reached = True
return self.retrace_path(current_node)
self.closed_nodes.append(current_node)
successors = self.get_successors(current_node)
for child_node in successors:
if child_node in self.closed_nodes:
continue
if child_node not in self.open_nodes:
self.open_nodes.append(child_node)
else:
# retrieve the best current path
better_node = self.open_nodes.pop(self.open_nodes.index(child_node))
if child_node.g_cost < better_node.g_cost:
self.open_nodes.append(child_node)
else:
self.open_nodes.append(better_node)
if not (self.reached):
return [self.start.pos]
def get_successors(self, parent: Node) -> List[Node]:
"""
Returns a list of successors (both in the grid and free spaces)
"""
successors = []
for action in delta:
pos_x = parent.pos_x + action[1]
pos_y = parent.pos_y + action[0]
if not (0 <= pos_x <= len(grid[0]) - 1 and 0 <= pos_y <= len(grid) - 1):
continue
if grid[pos_y][pos_x] != 0:
continue
successors.append(
Node(
pos_x,
pos_y,
self.target.pos_y,
self.target.pos_x,
parent.g_cost + 1,
parent,
)
)
return successors
def retrace_path(self, node: Node) -> List[Tuple[int]]:
"""
Retrace the path from parents to parents until start node
"""
current_node = node
path = []
while current_node is not None:
path.append((current_node.pos_y, current_node.pos_x))
current_node = current_node.parent
path.reverse()
return path
if __name__ == "__main__":
init = (0, 0)
goal = (len(grid) - 1, len(grid[0]) - 1)
for elem in grid:
print(elem)
print("------")
greedy_bf = GreedyBestFirst(init, goal)
path = greedy_bf.search()
for elem in path:
grid[elem[0]][elem[1]] = 2
for elem in grid:
print(elem)
-
A∗ search: este algoritmo busca o menor caminho entre dois vértices de um grafo usando valores de duas funções responsáveis por estimar o melhor caminho em relação ao custo acumulado do caminho percorrido e o valor restante necessário até o destino. Sendo assim, a soma desses dois valores estimam o caminho mais eficiente entre o destino e a origem. Por fim, é importante considerar que, quanto menor for este valor, menos custoso será o trajeto calculado.
Vantagens: algoritmo muito eficiênte e garante uma solução ótima.
Desvantagens: usa muita memória e consideravelmente mais complexo que todos os outros algoritmos apresentados. O site GeegsForGeeks apresenta um bom exemplo de implementação.
Busca Complexa
Alguns problemas, como otimização e planejamento, possuem um alto grau de dificuldade em encontrar soluções. Como dito no artigo anterior Solução de Problemas em Inteligência Artificial, para estes problemas, as vezes é mais interessante preocupar-se apenas com o estado final, e não com o caminho até ele, sendo a Busca Local uma das principais abordagens utilizadas nessas situações.
Esse abordagem começa com uma solução inicial e faz pequenas alterações nela para melhorar progressivamente a solução por meio da exploração de soluções próximas. Para isso, ao considerar um espaço de estados, isto é, conjunto de todas as possíveis soluções viáveis para o problema, deve-se verificar a elevação: uma melhora ou aumento no valor da função objetivo.
Mas o que seria a Função Objetivo? Também conhecida como Função de Custo ela rerpesenta uma quantificação do desempenho das soluções possíveis para o problema. A Imagem 6 a seguir apresenta uma síntese desses conceitos em um plano cartesiano Função Objetivo X Espaço de Estado (contem os estados possíveis).
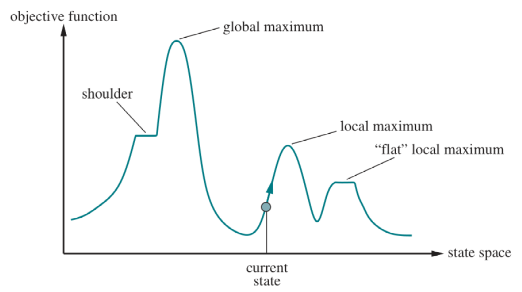
Ref.: material didático da disciplina de Inteligência Artificial da FGA (2023.2).
Diante do exposto, pode-se entender a busca local como um processo iterativo que vai continuamente de encontro à um valor cada vez maior de desempenho, sendo o fim do algoritmo determinado pelo encontro de um determinado pico, isto é, onde os valores vizinhos não possuem valor maior que o valor atual.
Este processo de busca pela solução de maior desempenho segue duas premissas principais: se a elevação corresponde a função objetivo, a meta é encontrar o maior pico (Hill Climbing), agora se a elevação corresponder ao custo, a meta é encontrar o vale mais baixo (gradient descent). Mas será que isso garante o encontro do maior pico possível? A resposta é depende. É nesse contexto que algumas técnicas se fazem presente. São elas:
- Escalada estocástica (Stochastic hill climbing): escolhe aleatoriamente os caminhos ascendentes;
- Escalada de primeira escolha (First-choice hill climbing): Escolhe sucessores aleatoriamente até que um melhor seja escolhido;
- Escalada com reinicialização aleatória (Random-restart hill climbing): executa diversos hill climbing iniciando em posições aleatórias;
- Recozimento simulado (Simulated annealing): Uma versão de stochastic hill climbing onde alguns movimento descendentes são permitidos
- Busca de feixe local (Local beam Search): O algoritmo acompanha k estados ao invés de apenas um;
Alguns outros algoritmos de busca
Além dos algoritmos apresentados até então, existem diversos outros algoritmos de busca cega, informada ou complexa, e o mesmo vale para os algoritmos genéticos. Sendo assim, este tópico apresentará alguns novos algoritmos, como o DLS (Depth-limited search), que consiste em uma variante da DFS que limita a profundidade da exploração, o Jump Search, que consiste em um algoritmo de busca que separa as informações em blocos e proucura no bloco mais próximo da solução e, por fim, o algoritmo genético conhecido como
-
DLS (Depth-limited search) - Busca Cega: funciona de maneira similar à DFS (Deph-Frist Search), com o acréscimo de uma restrição a qual limita ae onde poderá atravessar os nós, resolvendo eventuais problemas de caminho infinito da DFS.
Vantagens: as mesmas da DFS, com adição de proteção à caminhos infinitos e economia de memória.
Desvantagens: assim como a DFS, nem sempre garantirá uma solução
EXEMPLO
Grafo:
Ref.: Analtytics Vidhya
Implementação da solução em python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
"""
REF: https://www.analyticsvidhya.com/blog/2021/10/an-introduction-to-problem-solving-using-search-algorithms-for-beginners/
"""
graph = {
'A' : ['B','C'],
'B' : ['D', 'E'],
'C' : ['F', 'G'],
'D' : [],
'E' : [],
'F' : [],
'G' : []
}
def DLS(start,goal,path,level,maxD):
print('Level atual-->',level)
path.append(start)
if start == goal:
print("Teste de meta bem-sucedido")
return path
print('Falha no teste do nó de destino')
if level==maxD:
return False
print('Expandindo o nó atual',start)
for child in graph[start]:
if DLS(child,goal,path,level+1,maxD):
return path
path.pop()
return False
start = 'A'
goal = input('Insira o nó de destino: ')
maxD = int(input("Insira o limite máximo de profundidade: "))
print()
path = list()
res = DLS(start,goal,path,0,maxD)
if(res):
print("Caminho para o nó de destino disponível")
print("Caminho",path)
else:
print("Nenhum caminho disponível para o nó de destino em determinado limite de profundidade")
Saída:
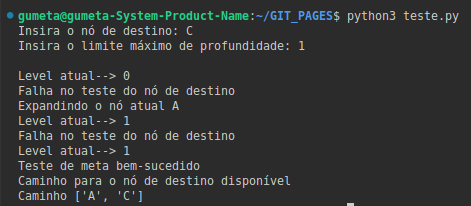
Ref.: autoria própria
-
Jump Search (Pesquisa de Blocos)- Busca Informada: funciona dividindo uma estrutura de dados (estática) em blocos de tamanho fixo e, em seguida, aplicando uma busca linear nos blocos até encontrar o bloco que provavelmente contém o valor desejado. Uma vez encontrado o bloco apropriado (mais próximo da solução), uma busca linear é realizada apenas nesse bloco, reduzindo o número de comparações necessárias. Contudo, para que isso seja possível, essa busca aproveita a informação de que a estrutura de dados está previamente ordenada, o que configura esse algoritmo como informado.
Vantagens: bastante eficiênte em estruturas de dados estáticas e não querer memória memória adicional significativa.
Desvantagens: precisa da garantia de que a estrutura esteja ordenada e torna-se cada vez mais ineficaz a medida em que os dados não estejam uniformemente distribuidos
EXEMPLO
Objetivo: encontrar o índice do elemento 55 dentro da array arr = [ 0, 1, 1, 2, 3, 5, 8, 13, 21,34, 55, 89, 144, 233, 377, 610 ].
Implementação da solução em python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
"""
REF: https://www.geeksforgeeks.org/jump-search/
"""
# Python3 code to implement Jump Search
import math
def jumpSearch( arr , x , n ):
# Finding block size to be jumped
step = math.sqrt(n)
# Finding the block where element is
# present (if it is present)
prev = 0
while arr[int(min(step, n)-1)] < x:
prev = step
step += math.sqrt(n)
if prev >= n:
return -1
# Doing a linear search for x in
# block beginning with prev.
while arr[int(prev)] < x:
prev += 1
# If we reached next block or end
# of array, element is not present.
if prev == min(step, n):
return -1
# If element is found
if arr[int(prev)] == x:
return prev
return -1
# Driver code to test function
arr = [ 0, 1, 1, 2, 3, 5, 8, 13, 21,
34, 55, 89, 144, 233, 377, 610 ]
x = 55
n = len(arr)
# Find the index of 'x' using Jump Search
index = jumpSearch(arr, x, n)
# Print the index where 'x' is located
print("Number" , x, "is at index" ,"%.0f"%index)
# This code is contributed by "Sharad_Bhardwaj".
Saída:

Ref.: autoria própria
-
Algoritmo Genético para Otimização Contínua de Funções - Algoritmo Genético: uma classe de algoritmos de busca heurística que visam encontrar a melhor solução para um problema de otimização de funções. Como dito anteriormente, esses algoritmos são inspirados na teoria da evolução e na genética, onde os princípios de seleção natural são aplicados a soluções candidatas para encontrar a solução ótima ou aproximadamente ótima para um problema.
Vantagens: exploração eficiente do espaço de busca em ambientes complexos e se adapta para múltiplos objetivos
Desvantagens: não garante solução ótima e possui uma configuração sensível, isto é, altamente dependente da escolha adequada dos parâmetros (tamanho da população, taxa de mutação, etc).
EXEMPLO
Objetivo: encontrar o valor mínimo da função f(x) = x^2 + y^2. (Vmin = f(0,0) = 0,0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
"""
# genetic algorithm search for continuous function optimization
REF: https://machinelearningmastery.com/simple-genetic-algorithm-from-scratch-in-python/
"""
from numpy.random import randint
from numpy.random import rand
# objective function
def objective(x):
return x[0]**2.0 + x[1]**2.0
# decode bitstring to numbers
def decode(bounds, n_bits, bitstring):
decoded = list()
largest = 2**n_bits
for i in range(len(bounds)):
# extract the substring
start, end = i * n_bits, (i * n_bits)+n_bits
substring = bitstring[start:end]
# convert bitstring to a string of chars
chars = ''.join([str(s) for s in substring])
# convert string to integer
integer = int(chars, 2)
# scale integer to desired range
value = bounds[i][0] + (integer/largest) * (bounds[i][1] - bounds[i][0])
# store
decoded.append(value)
return decoded
# tournament selection
def selection(pop, scores, k=3):
# first random selection
selection_ix = randint(len(pop))
for ix in randint(0, len(pop), k-1):
# check if better (e.g. perform a tournament)
if scores[ix] < scores[selection_ix]:
selection_ix = ix
return pop[selection_ix]
# crossover two parents to create two children
def crossover(p1, p2, r_cross):
# children are copies of parents by default
c1, c2 = p1.copy(), p2.copy()
# check for recombination
if rand() < r_cross:
# select crossover point that is not on the end of the string
pt = randint(1, len(p1)-2)
# perform crossover
c1 = p1[:pt] + p2[pt:]
c2 = p2[:pt] + p1[pt:]
return [c1, c2]
# mutation operator
def mutation(bitstring, r_mut):
for i in range(len(bitstring)):
# check for a mutation
if rand() < r_mut:
# flip the bit
bitstring[i] = 1 - bitstring[i]
# genetic algorithm
def genetic_algorithm(objective, bounds, n_bits, n_iter, n_pop, r_cross, r_mut):
# initial population of random bitstring
pop = [randint(0, 2, n_bits*len(bounds)).tolist() for _ in range(n_pop)]
# keep track of best solution
best, best_eval = 0, objective(decode(bounds, n_bits, pop[0]))
# enumerate generations
for gen in range(n_iter):
# decode population
decoded = [decode(bounds, n_bits, p) for p in pop]
# evaluate all candidates in the population
scores = [objective(d) for d in decoded]
# check for new best solution
for i in range(n_pop):
if scores[i] < best_eval:
best, best_eval = pop[i], scores[i]
print(">%d, new best f(%s) = %f" % (gen, decoded[i], scores[i]))
# select parents
selected = [selection(pop, scores) for _ in range(n_pop)]
# create the next generation
children = list()
for i in range(0, n_pop, 2):
# get selected parents in pairs
p1, p2 = selected[i], selected[i+1]
# crossover and mutation
for c in crossover(p1, p2, r_cross):
# mutation
mutation(c, r_mut)
# store for next generation
children.append(c)
# replace population
pop = children
return [best, best_eval]
# define range for input
bounds = [[-5.0, 5.0], [-5.0, 5.0]]
# define the total iterations
n_iter = 100
# bits per variable
n_bits = 16
# define the population size
n_pop = 100
# crossover rate
r_cross = 0.9
# mutation rate
r_mut = 1.0 / (float(n_bits) * len(bounds))
# perform the genetic algorithm search
best, score = genetic_algorithm(objective, bounds, n_bits, n_iter, n_pop, r_cross, r_mut)
print('Done!')
decoded = decode(bounds, n_bits, best)
print('f(%s) = %f' % (decoded, score))
Saída:
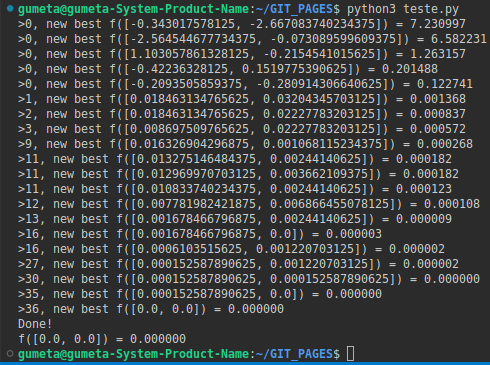
Ref.: autoria própria
Conclusão
Diante do exposto, percebe-se os algoritmos de busca possuem uma ampla gama de aplicações, além de poderem ser divididos em grupos de classificação, como algoritmos de busca cega, informada e complexa, havendo vantagens e desvantagens para cada um deles. Não obstante, em problemas de alto nível de complexidade como otimização, algoritmos genéticos e algoritmos de busca local são ótimas opções, havendo diversas técnicas de implementação de cada um desses dois tipos de algoritmos, sendo elas escolhidas de acordo com o problema a ser resolvido. Logo, pode-se dizer que tais algoritmos são fundamentais para as tecnologias de inteligência artificial, impactando diretamente na solução de diversos problemas.
Impressões Finais do Autor
Eu, como estudante de Engenharia de Software e amante de algoritmos de computadores, me vi muito interessado sobre o conteúdo abordado desde o início. Aprendi algumas utilidades novas para algoritmos de busca que aprendi no passado, assim como entrei em contato com novos algoritmos os quais expandem minhas ferramentas de solução de problemas, como o caso dos algoritmos genéticos. Aprendi que a solução de problemas por meio de agentes envolve diversas áreas do conhecimento dentro do universo da computação, como algoritmos de busca e suas aplicações, as quais variam de acordo com o contexto. Por fim, vale ressaltar que fiquei bastante intrigado com o biomimetismo dos algoritmos genéticos, pois provam mais uma vez a grande capacidade humana de observar a natureza e imita-la para criação de tecnologias e soluções de problemas.
Referências Bibliográficas
ALGORITMO genético simples do zero em Python. [S. l.], 12 out. 2021. Disponível em: https://machinelearningmastery.com/simple-genetic-algorithm-from-scratch-in-python/. Acesso em: 29 out. 2023.
JUMP Search. [S. l.], 25 abr. 2023. Disponível em: https://www.geeksforgeeks.org/jump-search/. Acesso em: 28 out. 2023.
BEST First Search: Informed Search. [S. l.], 21 fev. 2023. Disponível em: https://www.geeksforgeeks.org/best-first-search-informed-search/. Acesso em: 28 out. 2023.
A* Search Algorithm. [S. l.], 8 mar. 2023. Disponível em: https://www.geeksforgeeks.org/a-search-algorithm/. Acesso em: 29 out. 2023.
AN Introduction to Problem-Solving using Search Algorithms for Beginners. [S. l.]. Disponível em: https://www.analyticsvidhya.com/blog/2021/10/an-introduction-to-problem-solving-using-search-algorithms-for-beginners/. Acesso em: 28 out. 2023.
BEST First Search in Artificial Intelligence. [S. l.]. Disponível em: https://www.analyticsvidhya.com/blog/2023/09/best-first-search-in-artificial-intelligence/. Acesso em: 28 out. 2023.
ENGENHARIA HÍBRIDA. Placas Eletrônicas (PCB/PCI): O que são e para que servem?. [S. l.], 17 out. 2023. Disponível em: https://www.engenhariahibrida.com.br/post/placas-eletronicas-o-que-sao-para-que-servem. Acesso em: 27 out. 2023.
PROBLEMA do caixeiro-viajante. [S. l.], 19 jun. 2023. Disponível em: https://pt.wikipedia.org/wiki/Problema_do_caixeiro-viajante. Acesso em: 27 jan. 2023.
GO. [S. l.], 13 out. 2023. Disponível em: https://pt.wikipedia.org/wiki/Go. Acesso em: 27 out. 2023.
ALGORITMOS de Busca para Inteligência Artificial. [S. l.], 3 jul. 2020. Disponível em: https://ricardomatsumura.medium.com/algoritmos-de-busca-para-intelig%C3%AAncia-artificial-7cb81172396c. Acesso em: 26 out. 2023.
ALGORITMOS GENÉTICOS: PRINCÍPIOS E APLICAÇÕES. ICA: Laboratório de Inteligência Computacional Aplicada, [s. l.]. Disponível em: https://www.inf.ufsc.br/~mauro.roisenberg/ine5377/Cursos-ICA/CE-intro_apost.pdf. Acesso em: 25 out. 2023.