“A imaginação é mais importante que o conhecimento. O conhecimento é limitado, enquanto a imaginação abraça o mundo inteiro, estimulando o progresso, e dando origem à evolução.” - Albert Einstein
Impressões Iniciais
No âmbito da inteligência artificial, a representação eficiente do conhecimento e o raciocínio lógico desempenham papéis essenciais. Ao estudar tais assuntos, emergem conceitos fundamentais que moldam a capacidade dos sistemas de IA em compreender e interagir com o mundo. Diante disso, o presente artigo possui o intúito de instruir o leitor um pouco mais sobre esse mundo, considerando aspectos como agentes baseados em conhecimento, lógica, inferência e, por fim, agentes baseados em lógica proposicional.
Agente Baseado em Conhecimento
Na área de Inteligência Artificial (IA), os agentes baseados em conhecimento utilizam um processo de raciocínio, ponderando sobre representações internas para tomar decisões. No entanto, os agentes atuais têm conhecimento limitado e inflexível. Somado a isso, a lógica é adotada como uma classe geral de representações para respaldar esses agentes, sendo a base de conhecimento (KB) seu componente central. A KB é composta por um conjunto de sentenças que expressam afirmações sobre o mundo, chamadas axiomas quando aceitas sem derivação. Essas sentenças são formuladas em uma linguagem de representação de conhecimento. Operações cruciais, como TELL para adicionar e ASK para consultar a KB, permitem a evolução do conhecimento.
Não obstante, a inferência, que é a capacidade de derivar novas sentenças, é fundamental e segue o requisito de consistência. Adicionalmente, duas abordagens para construir a KB são destacadas: a declarativa, onde o projetista especifica sentenças uma a uma, e a procedural, que codifica comportamentos desejados diretamente como código de programa. Esses elementos essenciais constituem a base para o funcionamento eficaz dos agentes baseados em conhecimento em sistemas de IA.
De acordo com o artigo A história da AI, Bert Raphael propôs ao mundo uma ideia conhecida como blocks world problem (problemas de micro-mundo), usado como caso de teste em pesquisas sobre sistemas de IA e lógica. Um bom exemplo de micromundo para ilustrar a aplicação de agentes baseados em conhecimento é o Wumpus World. Nele, há uma caverna a qual é composta por câmaras conectadas por passagens, onde um temível monstro, o Wumpus, reside em alguma parte. O agente, munido de apenas uma flecha, pode eliminar o Wumpus, mas deve ser cauteloso, pois algumas câmaras abrigam poços mortais. Além disso, há um tesouro escondido em alguma câmara. Os elementos fundamentais incluem atuadores, uma medida de performance, um ambiente com sensores e um agente único.
O Wumpus World é determinístico, discreto, estático e de agente único. Sua natureza sequencial implica que a recompensa é obtida após uma série de ações. No entanto, o ambiente é parcialmente observável, apresentando desafios adicionais ao agente. Este cenário proporciona uma base prática para compreender como agentes baseados em conhecimento operam em ambientes complexos, tomando decisões informadas para maximizar o desempenho em meio a incertezas. Confira a Imagem 1 a seguir a qual carrega um exemplo de caverna no micro-mundo Wumpus World.
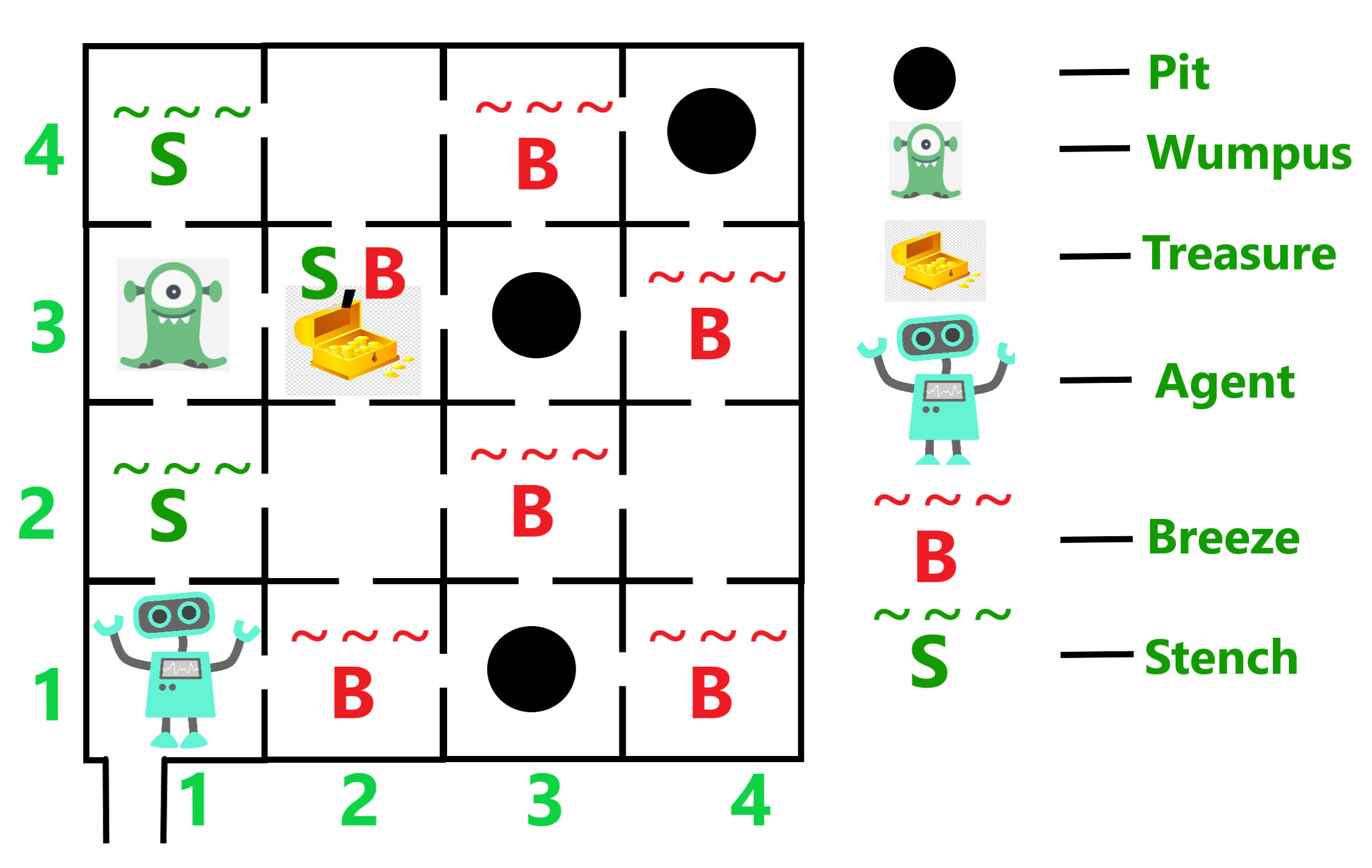
Ref.: Geeksforgeeks
Lógica
A lógica abrange diversos elementos essenciais na análise linguística e raciocínio formal, podendo ser expressa por meio de sintaxe, sentenças e semânticas. A sintaxe, componente do sistema linguístico, estabelece as relações formais na estrutura das sentenças. Já as sentenças bem construídas seguem essa estrutura, enquanto sentenças mal construídas a violam. A semântica, por sua vez, lida com o sentido das palavras e a interpretação de sentenças, definindo a verdade em diferentes contextos.
Para uma sentença α ser verdadeira em um modelo m, dizemos que m satisfaz α. A relação lógica entre sentenças, denotada por α ⊨ β, indica que α implica β, e a verdade de β depende da verdade de α. A implicação e a inferência lógica (processo de dedução ou conclusão lógica de informações novas com base em informações existentes) são expressas pela inclusão de conjuntos de modelos: α⊨β se e somente se o conjunto de modelos de α está contido no conjunto de modelos de β. Este raciocínio lógico pode ser aplicado em contextos como o mundo wumpus, exemplificando a aplicação prática desses conceitos.
Na lógica, a notação 1, conforme mostra a imagem 2 a baixo, indica que um algoritmo de inferência i pode derivar α da base de conhecimento KB, ou seja, α é obtido por meio de i a partir KB.
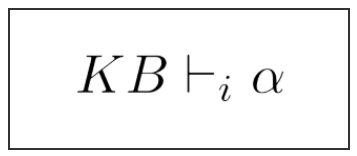
Ref.: autoria própria.
Um algoritmo de inferência é considerado completo se pode derivar qualquer sentença relacionada à base de conhecimento. Sendo assim, podemos utilizar a sintaxe da lógica proposicional, um ramo da lógica que estuda a manipulação de proposições, que são afirmações ou declarações que podem ser verdadeiras ou falsas. Nesse sistema, as proposições são representadas por símbolos, como A, B ou C, e são combinadas utilizando conectivos lógicos, como:
∧ (AND)
∨ (OU)
¬ ou ~ (NÃO)
⇒ (IMPLICA)
⇔ (SE e SOMENTE SE)
⊕ (OU EXCLUSIVO).
Outra ferramenta interessante é a gramática BNF (Backus–Naur Form), a qual é usada para definir a estrutura de sentenças em lógica proposicional, considerando precedências de operadores da mais alta prioridade para a mais baixa.
Por fim, a semântica estabelece regras para determinar a verdade de uma sentença em relação a um modelo específico. Para sentenças complexas, cinco regras se aplicam a quaisquer sub-sentenças A e B em qualquer modelo m (considerando sse como se e somente se). São elas:
¬A é verdadeiro sse A é falso em m.
A∧B é verdadeiro sse A e B são verdadeiros em m.
A∨B é verdadeiro sse A ou B for verdadeiro em m.
A ⇒ B é verdadeiro, a menos que A seja verdadeiro e B seja falso em m.
A ⇔ B é verdadeiro sse A e B são ambos verdadeiros ou ambos falsos em m.
Confira a Imagem 3 a baixo, a qual representa uma tabela verdade para os valores de A e B de acordo com as regras a cima:
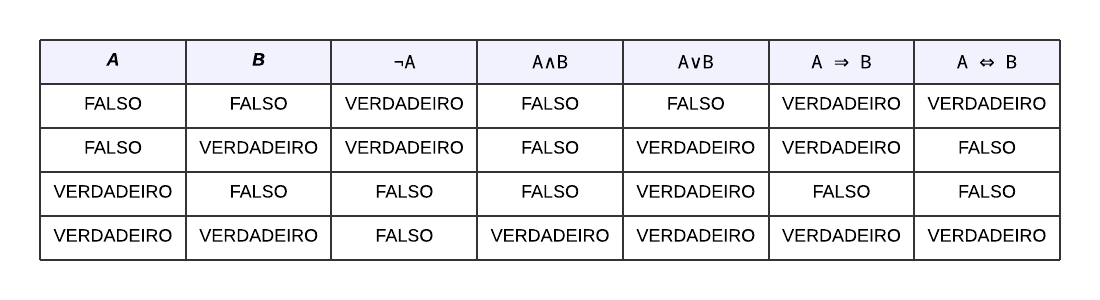
Ref.: autoria própria.
Processo de Inferência
Como visto, a inteligência artificial (IA) pode fazer o uso de uma base de conhecimento (KB) na qual são armazenadas afirmações sobre o mundo. Sendo assim, o processo de inferência em IA é uma ferramenta que envolve o raciocínio sobre essa base para tomar decisões e, para isso, utiliza-se de equivalência lógica (≡): duas sentenças são equivalentes se são verdadeiras para o mesmo conjunto de modelos. (Ex.: A v B ≡ B v A)
Outro conceito importanté é a validade de uma sentença, chamada de tautologia, a qual ocorre quando é verdadeira em todos os modelos. Por outro lado, existe um teroema muito importante denominado Teorema da Dedução o qual afirma que uma sentença β é consequência de α se e somente se α implica em β. Isso se relaciona com a validade e satisfatibilidade que, por sua vez, consiste em determinar que uma sentença é satisfazível se for verdadeira em algum modelo.
Existem diversas outras ferramentas utilizadas na lógica, tais como o método de prova conhecido como reductio ad absurdum (redução por contradição/absurdo), que busca estabelecer a veracidade de uma afirmação ao assumir o contrário dela e, em seguida, demonstrar que essa suposição levaria a uma contradição ou a uma conclusão absurda. Outras técnicas como o Modus Ponens e a Eliminação por Conjunção são regras de inferência sólidas que formam a base para derivar outras regras, sendo a completude dos algoritmos de inferência, especialmente em estratégias como a busca de aprofundamento iterativo, crucial para garantir que todas as soluções alcançáveis sejam encontradas. Confira a seguir uma explicação mais detalhada dessas regras.
1 - Modus Ponens: se há uma sentença condicional do tipo "Se A ⇒ B" e sabemos que A é verdadeiro, então podemos inferir que B também é verdadeiro. Isso pode ser escrito da seguinte forma:
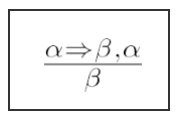
Ref.: autoria própria.
2 - Eliminação por Conjunção (And-Elimination): se soubermos que uma conjunção (por exemplo, A ∧ B) é verdadeira, podemos inferir que cada componente individual (A e B) também é verdadeiro. Isso pode ser escrito da seguinte forma:
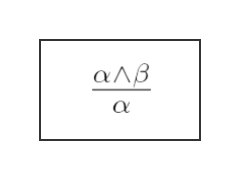
Ref.: autoria própria.
Um bom exemplo de regra derivada do Modus Ponens e da Eliminação por Conjunção é a Eliminação Bicondicional. Nela, o bicondicional (↔) entre duas sentenças, por exemplo, α ↔ β, pode ser expresso como (α → β) ∧ (β → α).
Por fim, vale ressaltar que os algoritmos de pesquisa, como a pesquisa de aprofundamento iterativo, garantem completude ao encontrar qualquer objetivo atingível. No entanto, se as regras de inferência disponíveis são inadequadas, conclui-se que o objetivo não é alcançável, pois não há uma prova possível utilizando apenas essas regras. Além disso, existe uma regra denominada inferência por resolução, a qual é usada para inferir novas cláusulas a partir de cláusulas existentes. Esta regra opera identificando dois literais complementares (um é a negação do outro) em diferentes cláusulas e removendo-os, resultando em uma nova cláusula que contém os literais restantes (resolução de unidade).
A regra de inferência por resolução, quando combinada com um algoritmo de procura, forma um algoritmo de inferência completo. Essa regra pode ser generalizada para a resolução total, onde duas cláusulas produzem uma nova contendo todos os literais das cláusulas originais, exceto os complementares. Tal cláusula resultante deve conter apenas uma cópia de cada literal, e a remoção de múltiplas cópias é chamada de fatoração. Essas estratégias são essenciais para uma inferência lógica eficaz.
Agente baseado em Lógica Proposicional
Um Agente baseado em Lógica Proposicional refere-se a um agente de inteligência artificial que utiliza a lógica proposicional como base para representar o conhecimento e realizar inferências. Nesse contexto, a lógica proposicional é uma forma de lógica que lida com proposições ou declarações que podem ser verdadeiras ou falsas. Esse tipo de agente utiliza regras de inferência lógica para processar informações, tomar decisões e agir no ambiente.
As implicações desse tipo de agente incluem a capacidade de representar conhecimento de maneira declarativa, expressar relações lógicas entre proposições e realizar inferências para tomar decisões. No entanto, a lógica proposicional tem suas limitações, pois lida apenas com sentenças simples, sem considerar a estrutura interna das proposições. Isso significa que, embora seja eficaz para representar conhecimento em domínios específicos, pode ser menos expressiva em comparação com formas mais avançadas de representação de conhecimento, como a lógica de primeira ordem (ou cálculo de predicados de primeira ordem). Portanto, a escolha de um agente baseado em lógica proposicional dependerá da natureza do problema e da complexidade das relações a serem representadas e inferidas.
Conclusões
Neste artigo, foram abordados uma variedade de conceitos fundamentais relacionados à representação de conhecimento e raciocínio lógico. De início, foram abordados os agentes baseados em conhecimento, cuja capacidade de tomar decisões é fundamentada em processos de raciocínio sobre representações internas. Somado a isso, tais esses agentes utilizam a lógica como uma classe geral de representações para respaldar suas operações, sendo a base de conhecimento o componente central. Essa base, composta por sentenças que afirmam algo sobre o mundo, é manipulada por operações como TELL e ASK, permitindo a evolução do conhecimento por meio da inferência, sendo o problema de micromundo do Wumpus, um bom exemplo prático para aplicar esses conceitos.
Não obstante, a lógica proposicional, a qual utiliza-se de conectores lógicos como ∧ (AND), ∨ (OU), ⇒ (IMPLICA), ⇔ (SE e SOMENTE SE), ⊕ (OU EXCLUSIVO) e outros, se mostrou uma ferramenta crucial para a representação de sentenças de diferentes níveis de complexidade. Somado a isso, a semântica, que define as regras para determinar a verdade das sentenças em relação a modelos, foi explorada, assim como as regras de inferência sólidas, como o Modus Ponens e a Eliminação por Conjunto. Por fim, foram abordadas as implicações práticas desses conceitos em inferência por resolução, resolução de unidade e fatoração.
Por fim, é possivel concluir que algoritmos como a pesquisa de aprofundamento iterativo são completos, capazes de alcançar objetivos, desde que as regras de inferência disponíveis sejam adequadas. Em resumo, ao percorrer esses conceitos fundamentais, aprende-se as bases que sustentam a capacidade dos sistemas de IA em representar conhecimento, raciocinar logicamente e tomar decisões informadas.
Referências
SISTEMAS Inteligentes: Agentes Lógicos. [S. l.], 21 out. 2023. Disponível em: https://www.inf.ufsc.br/~alexandre.goncalves.silva/courses/14s2/ine5633/slides/aula1021.pdf. Acesso em: 13 nov. 2023.
AGENTES Baseados na Lógica Proposicional. [S. l.], 2014. Disponível em: https://slideplayer.com.br/slide/2262895/. Acesso em: 13 nov. 2023.
LÓGICA de primeira ordem. [S. l.], 2 set. 2022. Disponível em: https://pt.wikipedia.org/wiki/L%C3%B3gica_de_primeira_ordem. Acesso em: 13 nov. 2023.